![Solution: a-1≥0, a≥1 introduces parameters x, y, z, sz=(a+8)/3√[(a-1)/3]x=³√(a+z)y=³√(a-z)s=x+y∴Original formula =s=x+y=³√(a+z)+³√(a-z)∴x³+y³=2a…①xy=³√(a²-z²)…② From ①:x³+y³=(x+y)(x²+y²-xy)=( - DayDayNews](https://cdn-dd.lujuba.top/img/loading.gif)
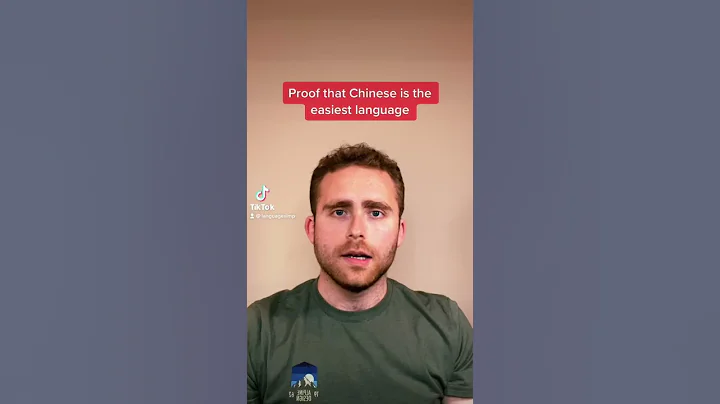
Solution: a-1≥0, a≥1
Introduce parameters x, y, z, s
z=(a+8)/3√[(a-1)/3]
x=³√(a+z)
y=³√(a-z)
s=x+y
s=x+y
∴Original formula=s=x+y=³√(a+z)+³√(a-z)
∴x³+y³=2a…①
xy=³√(a²-z²)…②
from ①:x³+y³=(x+y)(x²+y²-xy)=(x+y)³-3xy(x+y)=(x+y)³-3xy(x+y)=(x+y)³-3³√(a²-z²)(x+y)=2a
∵a²-z²=a²-z²)(x+y)=2a
∵a²-z²=a²-z²)(x+y)=2a
∵a²-z²=a²-z²)(x+y)=2a
∵a²-z²=a²-(a²+16a+64)(a-1) /27
=a²-(a³-a²+16a²-16a²-16a+64a-64)/27
=-(a³-12a²+48a-64)/27
=-(a-4)³/27=(4-a)³/27
∴³√(a²-z²)=³√[(4-a)/3]³=(4-a)/3
∴(x+y)³+(a-4) (x+y)-2a=0
∴(x+y)³+(a-4) (x+y)-2a=0
html l0∵s=x+y
∴s³+(a-4)s-2a=0
∴(s³-8)+(a-4)s-2(a-4)=0
∴(s-2)(s²+2s+4)+(a-4)(s-2)=0
∴(s-2)(s²+2s+a)=0
∴s1=2, s2=-2+√(1-a), s3=-2-√(1-a)(a≥1)